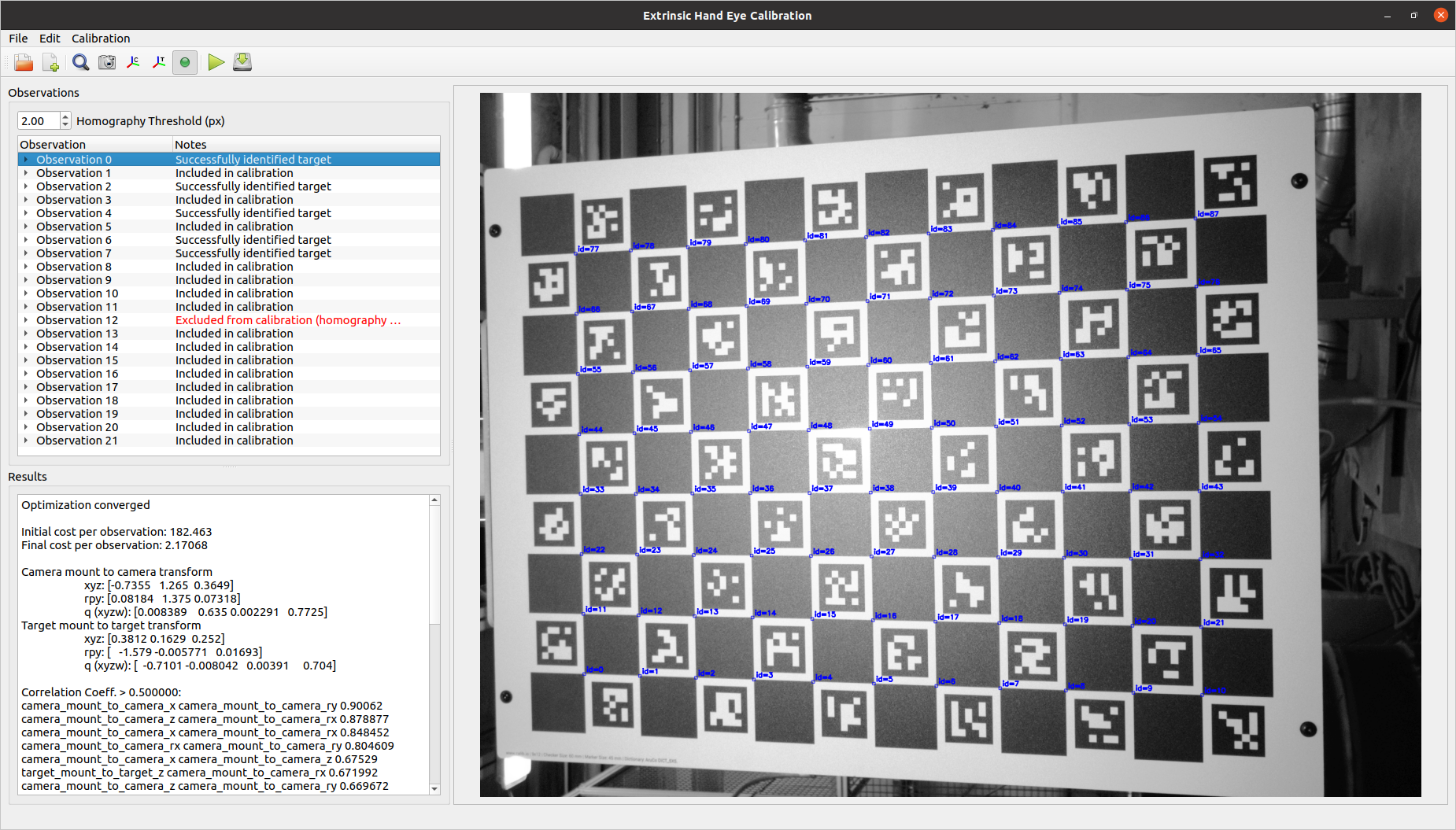
This application performs extrinsic hand-eye calibration based on 2D camera images and measured camera/target poses. The application requires a file that specifies the configuration of the calibration problem and the observation data to be used in the calibration. The outputs of this calibration are:

optimized estimate of the transform from the camera mount frame to the camera frame
optimized estimate of the transform from the target mount frame to the target frame

See also: ExtrinsicHandEyeCalibrationWidget

Running the Application

Run the application by executing the compiled executable from the install directory of the colcon workspace in which it was built:

source <workspace>/install/setup.bash

./<workspace>/install/industrial_calibration/bin/industrial_calibration_extrnisic_hand_eye_calibration_app

industrial_calibration

Definition camera_intrinsic_calibration_analysis.h:7

Alternatively, use ROS2 to start the application:

source <workspace>/install/setup.bash

ros2 run industrial_calibration industrial_calibration_extrnisic_hand_eye_calibration_app

Observation Definition

The observation data for this application consists of:

Pose measurements, saved to a YAML file
- from the camera mount frame to the camera frame, for applications where the camera is moving, or
- from the target mount frame to the target frame, for applications where the camera is static
2D image files in OpenCV-compatible formats (e.g., .png, .jpg, etc.)

The observation data and YAML file can be generated by the calibration data collector node in industrial_calibration_ros. Alternatively, users can collect calibration data manually and generate the observation YAML file by hand.

Pose files should be specified as a position vector in meters and quaternion, in the following format:

x:  0.0  # (m)
y:  0.0  # (m)
z:  0.0  # (m)
qx: 0.0
qy: 0.0
qz: 0.0
qw: 1.0

The observations should be collated into a YAML file (e.g., cal_data.yaml) that lists each corresponding pair of image and pose files. The image and pose files should be specified by their local directory, relative to the location of this file.

data:
  - image: <relative>/<path>/<to>/<image>
    pose:  <relative>/<path>/<to>/<pose>/<file>
  - image: ...
    pose:  ...
  - image: ...
    pose:  ...

Configuration Definition

Additional configuration information about the system also needs to be provided in order to perform the calibration. The configuration can be generated and saved to YAML file from the GUI using the icons and menu options. The format of the YAML configuration file is as follows:

camera_intrinsics

Camera intrinsic parameters for a pinhole model camera, without distortion

camera_mount_to_camera_guess

Initial guess for the transform from the camera mount frame to the calibrated camera frame

target_mount_to_target_guess

Initial guess for the transform from the target mount frame to the calibrated target frame

target_finder

Plugin configuration for target finder used to detect the calibration target in the image observations.

Here is an example configuration for a ModifiedCircleGridTargetFinder:

target_finder:
  type: ModifiedCircleGridTargetFinder
  rows: 10
  cols: 10
  spacing: 0.0254 # (meters between dot centers)
  circle_detector_params:
    minThreshold: 20
    maxThreshold: 220
    nThresholds: 20
 
    minRepeatability: 3
    circleInclusionRadius: 5
    maxRadiusDiff: 5
 
    maxAverageEllipseError: 0.02
 
    filterByColor: true
    circleColor: 0
 
    filterByArea: true
    minArea: 25.0
    maxArea: 5000.0
 
    filterByCircularity: false
    minCircularity: 0.8
    maxCircularity: 99999999.0
 
    filterByInertia: false
    minInertiaRatio: 0.1
    maxInertiaRatio: 99999999.0
 
    filterByConvexity: true
    minConvexity: 0.95
    maxConvexity: 99999999.0

Here is an example configuration for a CharucoGridBoardTargetFinder:

target_finder:
  type: CharucoGridTargetFinder
  rows: 7
  cols: 5
  chessboard_dim: 0.036195
  aruco_marker_dim: 0.018256
  dictionary: 10  # DICT_6X6_250

homography_threshold

In general, we want to ensure that the calibration target features observed in an image matches closely to the known geometry of the target. For planar calibration targets and 2D images, we can do this by computing a homography transform between the known target features and the observed target features. This homography transform projects the known target features onto the observed target features, allowing us to measure the average distance between corresponding features (in pixels). If the average homography error is above a specified threshold value, we want to exclude that observation from the calibration because the observed target match close enough to our known target geometry.

static_camera

Flag indicating whether the camera is static in the calibration

Example Configuration File

Here is an example of a calibration configuration YAML file:

# Camera intrinsics
intrinsics:
  fx: 1352.02747
  fy: 1356.14287
  cx: 789.67065
  cy: 627.2995
 
# Pose guesses
camera_mount_to_camera_guess:
  x:  0.0
  y:  0.0
  z:  0.0
  qx: 0.0
  qy: 0.0
  qz: 0.0
  qw: 1.0
target_mount_to_target_guess:
  x:  0.0
  y:  0.0
  z:  0.0
  qx: 0.0
  qy: 0.0
  qz: 0.0
  qw: 1.0
 
# Target finder
target_finder:
  type: <target finder plugin name>
  <target_finder_params>: ...
 
# Other parameters
homography_threshold: 2.0
static_camera: true

Tips for Getting an Accurate Calibration

Before Calibration

Verify that the dimensions of the physical calibration target match the parameters specified in the target detector configuration file
Verify that the camera intrinsic calibration is accurate. See Camera Intrinsic Calibration GUI Application for more details about performing camera intrinsic calibration.
Configure the camera to produce the largest possible image size
Configure the camera or image pipeline to produce rectified images

During Calibration

Take lots of samples in lots of different positions It's not uncommon to require tens of images from all over your workspace to get a good calibration.
Ensure the camera is fully stationary when acquiring images
Ensure the collected images are rectified
Acquire images in such a way that the calibration target takes up as much of the image as possible
Ensure the measurement of the transform from the target mount frame to the camera mount frame is as accurate as possible. For example, most robot manipulators will report their calibrated tool flange frames

Evaluating the Results

Residual Error

Residual error is the average squared error between the detected and expected target features remaining at the end of the calibration optimization. In the case of this optimization, the units of the residual error are squared pixels.

Note: The corresponding value reported in the GUI is the square root of the residual error, which is in the more meaningful units of pixels.

Residual error generally scales with the size (in pixels) of each target feature (e.g., a checkerboard intersection) in the image.

For example, in the case of a high resolution camera, a 10x10 neighborhood of pixels might represent a checkboard intersection. In a lower reslution camera, however, the same checkboard intersection might only be represented by a 2x2 neighborhood of pixels. Calibration with the high resolution camera will likely result in a higher residual error because a distance in physical space (e.g., mm) maps to a greater number of pixels in image space.

3D Reprojection Error

In addition to evaluating error in image space, it is possible to project that error back into physical 3D space (under the assumption that the calibration target is planar). Like residual error, this measure of error reports the average distance between a detected target feature and its expected location. However, this error metric is generally more meaningful than residual error because it reports average error in physical units (e.g., mm) and is not influenced by the resolution of the calibration images.

Comparison to PnP Optimizations

This calibration algorithm assumes that the measurement of the pose from the target mount frame to the camera mount frame ( 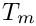$T_{m}$ ) is perfectly accurate. Generally this is not actually the case: robots are not perfectly rigid, models do not perfectly match as-built hardware, etc.

To understand the generally effect of this "perfect pose measurement" assumption, we run a PnP optimization for each acquired image and compare its reported camera-to-target transform ( 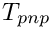$T_{pnp}$ ) to that predicted by this calibration ( $T_{cal}$ ). The PnP optimization simply tries to find the optimal placement of the camera relative to the target and is not constrained or influenced by the geometry of the robot holding the camera/target.

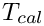
If the measurement of 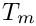$T_{m}$ is perfect, then the difference between $T_{pnp}$ and $T_{cal}$ should be similar to the 3D reprojection error. If the difference is significantly higher than the 3D reprojection error, this is an indication that $T_{m}$ may not have been accurate enough.

Correlation Coefficients

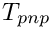
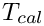
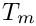
A correlation coefficient is a number on [-1, 1] describing how interrelated two variables are to one another.

A value of 0 means that a change in one variable has no effect on the second variable.
A value of 1 means that an increase in one variable produces the same size increase in the secibd variable.
A value of -1 means that an increase in one variable produces the same size decrease in the second variable.

In the context of a calibration optimization problem, ideally all calibration variables are independent of one another, and all correlation coefficients should therefore be 0.

In practice, this is generally not true, but all correlation coefficients should be relatively low. A very high correlation coefficient between any two variables (typically > 0.8) generally means that two variables play the same role in reducing the overall optimization cost and cannot be accurately distinguished from one another.

High correlation coefficients in the context of extrinsic hand-eye calibration typically indicate that not enough variety of camera poses were used for the calibration. To correct, add images from camera poses that look at the calibration target from a variety of different angles.